unflatten now has a free function version in torch.flatten in addition to
the method in torch.Tensor.flatten.
Updated docs to reflect this and polished them a little.
For consistency, changed the signature of the int version of unflatten in
native_functions.yaml.
Some override tests were failing because unflatten has unusual
characteristics in terms of the .int and .Dimname versions having
different number of arguments so this required some changes
to test/test_override.py
Removed support for using mix of integer and string arguments
when specifying dimensions in unflatten.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/81399
Approved by: https://github.com/Lezcano, https://github.com/ngimel
Currently we have 2 ways of doing the same thing for torch dispatch and function modes:
`with push_torch_dispatch_mode(X)` or `with X.push(...)`
is now the equivalent of doing
`with X()`
This removes the first API (which is older and private so we don't need to go through a deprecation cycle)
There is some risk here that this might land race with a PR that uses the old API but in general it seems like most are using the `with X()` API or `enable_torch_dispatch_mode(X())` which isn't getting removed.
EDIT: left the `with X.push(...)` API since there were ~3 land races with that over the past day or so. But made it give a warning and ask users to use the other API
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78215
Approved by: https://github.com/ezyang
This PR adds support for `SymInt`s in python. Namely,
* `THPVariable_size` now returns `sym_sizes()`
* python arg parser is modified to parse PyObjects into ints and `SymbolicIntNode`s
* pybind11 bindings for `SymbolicIntNode` are added, so size expressions can be traced
* a large number of tests added to demonstrate how to implement python symints.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78135
Approved by: https://github.com/ezyang
This PR heavily simplifies the code of `linalg.solve`. At the same time,
this implementation saves quite a few copies of the input data in some
cases (e.g. A is contiguous)
We also implement it in such a way that the derivative goes from
computing two LU decompositions and two LU solves to no LU
decompositions and one LU solves. It also avoids a number of unnecessary
copies the derivative was unnecessarily performing (at least the copy of
two matrices).
On top of this, we add a `left` kw-only arg that allows the user to
solve `XA = B` rather concisely.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/74046
Approved by: https://github.com/nikitaved, https://github.com/IvanYashchuk, https://github.com/mruberry
This PR adds `linalg.lu_solve`. While doing so, I found a bug in MAGMA
when calling the batched MAGMA backend with trans=True. We work around
that by solving the system solving two triangular systems.
We also update the heuristics for this function, as they were fairly
updated. We found that cuSolver is king, so luckily we do not need to
rely on the buggy backend from magma for this function.
We added tests testing this function left and right. We also added tests
for the different backends. We also activated the tests for AMD, as
those should work as well.
Fixes https://github.com/pytorch/pytorch/issues/61657
Pull Request resolved: https://github.com/pytorch/pytorch/pull/77634
Approved by: https://github.com/malfet
```Python
chebyshev_polynomial_v(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the third kind $V_{n}(\text{input})$.
```Python
chebyshev_polynomial_w(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the fourth kind $W_{n}(\text{input})$.
```Python
legendre_polynomial_p(input, n, *, out=None) -> Tensor
```
Legendre polynomial $P_{n}(\text{input})$.
```Python
shifted_chebyshev_polynomial_t(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the first kind $T_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_u(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the second kind $U_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_v(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the third kind $V_{n}^{\ast}(\text{input})$.
```Python
shifted_chebyshev_polynomial_w(input, n, *, out=None) -> Tensor
```
Shifted Chebyshev polynomial of the fourth kind $W_{n}^{\ast}(\text{input})$.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78304
Approved by: https://github.com/mruberry
Adds:
```Python
bessel_j0(input, *, out=None) -> Tensor
```
Bessel function of the first kind of order $0$, $J_{0}(\text{input})$.
```Python
bessel_j1(input, *, out=None) -> Tensor
```
Bessel function of the first kind of order $1$, $J_{1}(\text{input})$.
```Python
bessel_j0(input, *, out=None) -> Tensor
```
Bessel function of the second kind of order $0$, $Y_{0}(\text{input})$.
```Python
bessel_j1(input, *, out=None) -> Tensor
```
Bessel function of the second kind of order $1$, $Y_{1}(\text{input})$.
```Python
modified_bessel_i0(input, *, out=None) -> Tensor
```
Modified Bessel function of the first kind of order $0$, $I_{0}(\text{input})$.
```Python
modified_bessel_i1(input, *, out=None) -> Tensor
```
Modified Bessel function of the first kind of order $1$, $I_{1}(\text{input})$.
```Python
modified_bessel_k0(input, *, out=None) -> Tensor
```
Modified Bessel function of the second kind of order $0$, $K_{0}(\text{input})$.
```Python
modified_bessel_k1(input, *, out=None) -> Tensor
```
Modified Bessel function of the second kind of order $1$, $K_{1}(\text{input})$.
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78451
Approved by: https://github.com/mruberry
Adds:
```Python
chebyshev_polynomial_t(input, n, *, out=None) -> Tensor
```
Chebyshev polynomial of the first kind $T_{n}(\text{input})$.
If $n = 0$, $1$ is returned. If $n = 1$, $\text{input}$ is returned. If $n < 6$ or $|\text{input}| > 1$ the recursion:
$$T_{n + 1}(\text{input}) = 2 \times \text{input} \times T_{n}(\text{input}) - T_{n - 1}(\text{input})$$
is evaluated. Otherwise, the explicit trigonometric formula:
$$T_{n}(\text{input}) = \text{cos}(n \times \text{arccos}(x))$$
is evaluated.
## Derivatives
Recommended $k$-derivative formula with respect to $\text{input}$:
$$2^{-1 + k} \times n \times \Gamma(k) \times C_{-k + n}^{k}(\text{input})$$
where $C$ is the Gegenbauer polynomial.
Recommended $k$-derivative formula with respect to $\text{n}$:
$$\text{arccos}(\text{input})^{k} \times \text{cos}(\frac{k \times \pi}{2} + n \times \text{arccos}(\text{input})).$$
## Example
```Python
x = torch.linspace(-1, 1, 256)
matplotlib.pyplot.plot(x, torch.special.chebyshev_polynomial_t(x, 10))
```
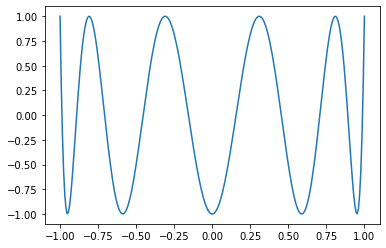
Pull Request resolved: https://github.com/pytorch/pytorch/pull/78196
Approved by: https://github.com/mruberry